メゾスコピック of ltlab

　マクロな領域(古典物理)とミクロな領域(量子物理)の中間(メゾ)領域であり、電子は波動性と粒子性を持つ量子状態となる。
これまでのテーマ
・ジョセフソン素子を用いたクーパー対のトンネリングやアンドレーエフ反射等の研究
・強磁性体を用いた微小接合系におけるスピン流の研究
・1/fノイズの研究　etｃ....
八木准教授のHPを参照

　試料が数ミクロン程度の場合、電極やリード線をはんだ等で直接試料に付けることができないため、波長の短い紫外線や電子線等を利用して基板上に電極パターンを描画する方法が用いられる。
　本グループでは、半導体の微細加工に用いられている電子線リソグラフィー技術により数μm～100nm程度の微細構造を作製している。
　加工には、電子線描画装置(SEM),　真空蒸着装置,　紫外線露光装置、プラズマエッチング装置を主として用いる。

◆電子線描画装置(SEM)によるパターン描画
　まず基板表面に、電子ビーム露光用の感光材(レジスト)をスピンコートにより均一に塗布する。
　この基板を、SEM内部に設置して設計したパターンに沿って電子ビームを照射する。
　その後、基板をSEMから取り出し、現像液に浸すと電子線の照射された箇所のレジストが除去される。
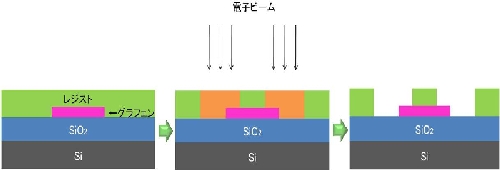順に、基盤表面にレジストを塗った状態、電子が当たったところだけを感光した状態、現像するとパターン部分のみレジストが取り除かれた状態
◆真空蒸着装置による金属の蒸着
　真空中で蒸着したい金属に熱電子を照射し金属を蒸発させる。この蒸発した金属を基板表面に付着させる。その後、レジストを有機溶媒等により除去すると描画したパターンのところに金属が残り、電極端子ができあがる。
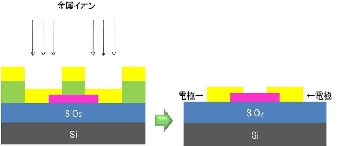左から順に、金属イオンが基盤表面に付着、レジストを取り除くとパターン部分のみ金属が残り、電極となる

　炭素は結合の仕方により様々な同素体を形成する。例えば、黒鉛・ダイアモンド(3次元)やカーボンナノチューブ(1次元)、フラーレン(0次元)等が知られている。
　2次元同素体であるグラフェンは、熱力学的に存在しないことが理論上示されていたが、2004年にGeim とNovoselovにより作製されて伝導特性が明らかにされた。
　このグラフェンは、層状構造をもつグラファイトの単原子層～数原子層でハニカム構造をもつ。そして、電子の振る舞いには、二次元性と相対論性がみられる。特に単層グラフェンはこの相対論的な特徴が顕著に現れるため積極的に研究されている。
グラファイト(左)とグラフェン(右)の結晶構造
◆グラフェン作製方法
　本研究室では、剥離法を用いてグラフェンの作製を行っている。
　まず、高純度の黒鉛表面をスコッチテープで剥離し、シリコン基板上に転写すると様々な層数のグラフェンが作製される。得られたグラフェンが何層であるかは、光学顕微鏡を通してグラフェンの色調を見ることで決定できる。これは、フレネルの法則を利用しており、数Åの厚みでも光の波長が変わり、写真にみられるグラフェンの層数に依存した色調の変化が観測される。
　この他にも化学気相成長(CVD)やSiCのエピタキシャル成長等による手法が開発されているが、上記の方法で作製したグラフェンの品質(移動度・配向性)が最も高いとされている。
グラファイト結晶からグラフェンを作製する様子
層数の違いによる見え方の違いグラフェン素子
◆グラフェンの特性
　上の図で示した結晶構造をもつ単層グラフェンは、ゼロギャップ半導体である。このバンド構造は、伝導帯と価電子帯が波数空間のK点においてディラック点と呼ばれる1点で線形に交わる。
　このためディラック点付近の電子は、放物線のバンド構造を記述するシュレディンガー方程式ではなく、線形のエネルギー分散を記述するディラック方程式に従って運動する。つまり、相対論的粒子であるフォトンやニュートリノと同じディラック粒子として振舞うことが考えられる。
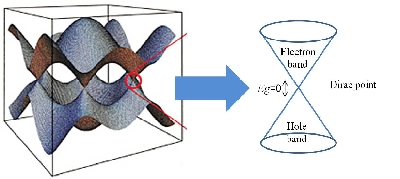グラフェンの3Dバンド構造
　グラフェンに特異的な物理現象として半整数量子ホール効果がある。　
　量子ホール効果(QHE)とは、ある磁場より大きくなるとサイクロトロン運動により物質内部の電子が離散的な状態(ランダウ量子化)を持ち、ホール伝導度にプラトーが生じる事である。
　通常の二次元物質ではホール伝導度は量子化伝導度を整数倍した値で量子化されるが、単層グラフェンでは幾何学的位相(ベリー位相)を反映して半整数の値にプラトーが生じる。
　量子化伝導度の係数は、一般的にスピンの自由度の2であるが、グラフェンの場合には単位胞に等価な2つの副格子を含むためにスピンと副格子の自由度を足し合わせて4つの自由度を持つ。
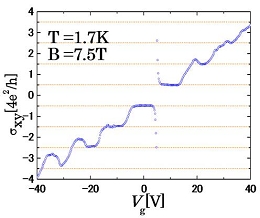半整数量子ホール効果
　また、単層と2層のグラフェンでは、通常の二次元系とは異なるランダウ準位が形成される。一般的な半導体では、N=0のランダウ準位は量子極限であり、各準位は等間隔に広がっている。そして、フェルミエネルギーがN=0以下になるとバンド構造が再配列される。
　グラフェンの場合にみられるランダウ準位を以下に示す。N=0に準位があり、これを中心に他の準位のエネルギー間隔はE=√N [単層の場合]　or √N(N-1)[2層の場合]に従い変化する。また、ゼロギャップ半導体であるため量子極限であるN=0の前後でエネルギーは連続的に変化する。
このランダウ準位はシュブニコフ・ド・ハース振動(S-dHO)を測定することで実験的に観測できる。試料に磁場をかけると準位間隔は広がっていくので高磁場領域では振動がはっきり見える。さらに、磁場を増大させることで、ゼーマン分裂によるスピンの分裂や副格子の分裂が生じることが観測されている。
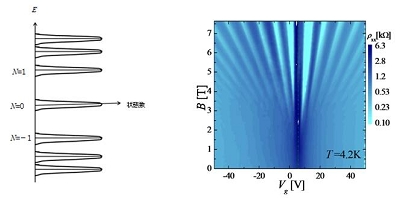左：グラフェンのランダウ準位、 右：ランダウ準位の広がりの様子 高抵抗の筋が各ランダウ準位に相当 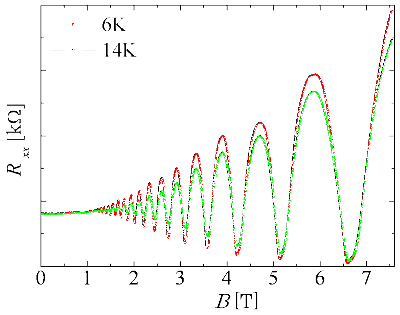シュブニコフ・ド・ハース振動(単層グラフェン)

　ランダウ量子化の他にもグラフェンは、様々な特徴を有している。2層グラフェンについては、価電子帯と伝導帯に放物線的なバンドがあり、フェルミ面付近で接する構造をもつ。また、垂直電場の印加によるエネルギーギャップの形成など注目すべき特性が多く見られる。3層グラフェンにおいては、積層構造によって、半金属と絶縁体の異なる状態をとるなどの特徴が見られている。
　このように、グラフェンは多様な特性を有しており、異なる層数のグラフェンを組み合わせることでカーボンエレクトロニクスへの応用が実現できる。しかし、グラフェンの問題点として不純物によって伝導特性の劣化が生じやすい事がある。
　この劣化は、界面に残留する不純物や基板の凹凸による格子の乱れに起因するため、グラフェンを宙づりにした素子構造を実現することで防ぐ事が可能である。これにより、以前より質の良い測定が可能となったため、本グループではグラフェン本来の伝導特性の解明に挑んでいる。
サスペンドの様子

グラフェンの特徴
1.シリコンより数100倍高い移動度をもつ。 (単層グラフェン)
2.可視光の透過率が、(100-2.3×層数)％で示される。
3.スピン-軌道相互作用が小さいため、スピン緩和時間が長い。
4.炭素間結合がsp2結合であるため、ダイアモンド（sp3結合）より丈夫。
5.銅の1000倍の電流密度耐性と10倍の熱伝導率を持つ。
6.厚みがÅのオーダーであるため柔軟性が高い。
7.表面積>>体積であるために、表面吸着により物性が大きく変化する。
8.既存の半導体微細加工技術を利用できる。
9.数100GHzの信号を低ノイズで伝搬可能。(2層グラフェン)
etc…。
現在行われている応用研究
高速・高周波半導体素子/ 量子デバイス(スピン,量子ビット)
透明導電膜(ディスプレイ,太陽電池) / センサー(化学,バイオ)　etc…。